WELDING OF ELECTRIC MOTOR

Those who have not yet acquired a welding machine (SA), I recommend you make it yourself on the basis of a failed induction motor. The cost is minimal, but the result… and development, which can be used for turning scrap stator in a good “svarochnik”, published a lot (see, for example, “modelist-Konstruktor” № 8’92, 11’95, 1’96, 3’96). I would be glad if someone useful to my practice-proven tips.

Experimenting with different CA, I was convinced that the pursuit of a powerful apparatus (typically for beginners) is not always economically justified. For most work at home is fine “svarochnik”, made on the basis of the stator asynchronous electric motor with capacity of 1 — 1.5 kW having a magnetic core with a cross section of 40 cm^2. To connect to home network 220 V with results for arc welding 40, 50 and 60 In the primary winding of such a must-have 220 turns and a secondary of 60, with taps on the 40th and 50th “bus” turns.

 

After the stator will be in your hands, take the time to cut or burn out the coil. Because it is in most cases quite suitable as source material for “mnogomernyh tire” required SA.

The stator winding of most induction motors is several overlapping sections. Laying each of them is made in the appropriate slots of the magnetic core. Inspect the stator to determine which sections were laid last. With her and start dismantling.

 

Knife for removing the wedges from the slots of the stator base of the motor.

 

Laying of turns of the tires rolled into the Bay, tor-magnetic circuit with reinforced insulation.

 

First of all, try to knock out the wedges (usually wood) that hold the windings fixed in the grooves. If this can not be done with the help of improvised means, use the device in the form of the knife a special configuration made from a cloth bench jigsaw.

 

The technology is simple. Moving the knife around on yourself, remove the chips from the wedge, ensuring the dismemberment….. After removal of the resulting debris begin loop for a loop to extract itself from the slots section. Do this carefully and slowly; in the reverse order of the original installation. With the release of the last partition unwind the wire and straighten, getting lengths of from 20 to 30 yards Of them and make the tire to the desired section.

 

Thus, to obtain bus primary (network) winding SA need to put together 3-6 wires-blanks so that the total section of copper wires made up of 6-8 mm^2. The resulting wiring should wrap the entire length with electrical tape on a fabric basis. Quite reasonable and a long insulating strips, stitched (glued) from scraps of linen or cotton. Will fit even paper tape, cut from, say, mail or cement bags.

To work on the production of the isolated tires were disputes, the original bundle of wires tie in several places with twine and roll into the Bay with a diameter of 600-800 mm. the tape overlap at an angle to the harness to each subsequent coil overlaps half of the previous, and the insulation was a double layer. Using cloth or paper, do not forget that these materials require subsequent impregnation with bakelite varnish or any (excluding latex) paint.

 

Similarly fabricate and bus to the secondary winding of the welding transformer. Here only wires in its composition must be so that the total section of copper wires was equal to 30-35 mm^2.

 

Now on the completion of the magnetic circuit. Its essence boils down to the base of the stator with a hammer and chisel to remove the jumpers between sections. And formed with sharp edges smooth with a file. The finished magnetic core is covered with several layers of insulation for the above technology.

 

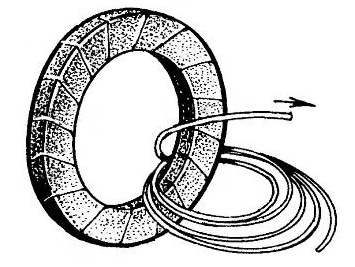
To facilitate the winding insert the cable into the core and rotate the ring until, until the last round will not be worn freely on tor-core “svarochnik”. Get as to two related heterogeneous link (steel yoke and copper coil) circuit.

 

The tire winding of the transformer to perform better together. First, clamp the vise to the edge of the yoke, then insert through the center of the torus the end of the bus, collapsed into the Bay, and, gently turning the last make got like two connected chain link. Securing the beginning of the primary winding on the surface of the torus with string, continue to rotate the tire, tightly stacking the coils on insulated magnetic core.

 

For the first layer of turns should be laying light weight insulation, impregnation the resulting “sandwich” liquefied bakelite varnish or diluted paint. Then a new layer of winding, distributed evenly across the surface of a torus with subsequent isolation. The coils are laid down strictly radially.

 

Completing primary (network) winding of the 220-th round. Next is the secondary (welding). Put it, after making a reinforced multilayer insulation. Just this winding, as already noted, 60 (with loop taps from 40 th and 50-th) of the coils.

 

General rule: if you suddenly found out that the wire (bus) is shorter than required, the increase should be performed outside of the winding, and properly filling out the appropriate conclusions.

 

Design improvised welding transformer depends on the capabilities of the author-artist. One of the most simple and acceptable variants— “side” consolidation “svarochnik” on an insulated base a simple clamp with a carrying handle.

P. BELOUSOV, Volgograd region