“The most cherished dream — height, height…” So goes the famous song about the pilots. Height — cherished dream and modelers-rocket, no matter what class competitions were athletic. For “tall” models it is a direct goal, and a planning and parasitisim dialed height guarantees good duration of the flight.
Ask any Modeler what needs to be done so that the model rose to the greatest height, and among the many the right answers is to reduce the aerodynamic drag, to supply the engine with a higher specific thrust, to ensure a good stabilization of the flight and the other will probably be this: “to Make the model as light as possible”. Seemingly right but actually a very light model can fly just as bad as and relatively heavy. Let’s call this phenomenon “the paradox of lightweight models” and try to understand its causes.
A model rocket belongs to the class of unguided ballistic missiles. The trajectory of their flight consists of two main sections: active, running engines, and passive, where the rocket flies like a brick thrown of an ancient throwing machine — a ballista. Trajectory motion of a rocket is the result of exposure to the different forces. What forces act on a rocket in flight!
Contact the authority, which itself had the opportunity to experience these forces. Listen, answers the question what forces have to deal with the rocket of the second Soviet envoy in space — Gherman Stepanovich Titov:
“First, with the engine thrust, and second, with the force of air resistance and, finally, with the weight of the rocket. Between these vultures, figuratively speaking, there is a struggle: the engine thrust causes the rocket forward, air resistance prevents it from movement and the weight of the rocket pulls down. In flight, the magnitude of these forces change. Changing the direction of their actions”.
What forces will have the advantage depends on the movement of the rocket and its final result — the flight path.
The forces acting on a rocket, on the active and passive sections are different. In the first case, the vertical take-off model the force of the engine thrust, directed upwards and dispersing it, as well as gravity and aerodynamic drag, braking the motion of a rocket and aimed down. Second — there are only two forces: drag and gravity.
The most complicated in the analysis of flight an active part of the trajectory: it changes not only the strength, but the mass of the rocket. Producing fuel, many modern rockets change their mass several times.
The change in mass of the rocket during its motion does not allow to use directly the formulas obtained in the classical mechanics of Newton. In the most rigorous, the approach to the study of the motion of bodies of variable mass was first considered by the famous Russian
a mechanic by I. V. Meshchersky. In his master thesis “Dynamics of point with variable mass,” written in 1897, he received a strict equation of motion of a body with variable mass under different hypotheses, rejecting masses. Regardless of Meshchersky as applied to missiles, investigated the motion of bodies of variable mass K. E. Tsiolkovsky. The theory of the motion of the rocket now called acetogenic, and Tsiolkovsky is considered the founder of modern rachitogenic.
Reflecting on the mysteries of the flight of the rocket, Tsiolkovsky was deep in a scientific way, consistently entering the main forces that affect the motion of a rocket. To find out the possibility the jet principle of movement of the bodies, the scientist considered the simplest task assumption: the flight of the rocket, which is valid only traction force. This task is now called the first task of Tsiolkovsky. One of its most important conclusions was that for the single-stage rarity speed at the end of the active portion will be larger, the larger the ratio of masses at the beginning and at the end of the flight.
Graphic method of determining altitude.
In the second task, Tsiolkovsky considered the vertical ascent of a rocket from the Earth, devoid of atmosphere. The analysis showed that the active height of the rocket will also increase with increasing the ratio of its initial mass and the final.
The real flight of the rocket in the air makes it difficult so that you can get the solution in the form of simple formulas fails and accurately calculate the motion of a rocket under the action of all three forces have learned relatively recently, using “abacus the XX century” — electronic computers. However, qualitatively the conclusions of the first and second tasks Tsiolkovsky remains valid for vertical lift rockets or model in the atmosphere: with the growth of the ratio of the initial and final masses increase both speed and height at the end of the active portion of the trajectory.
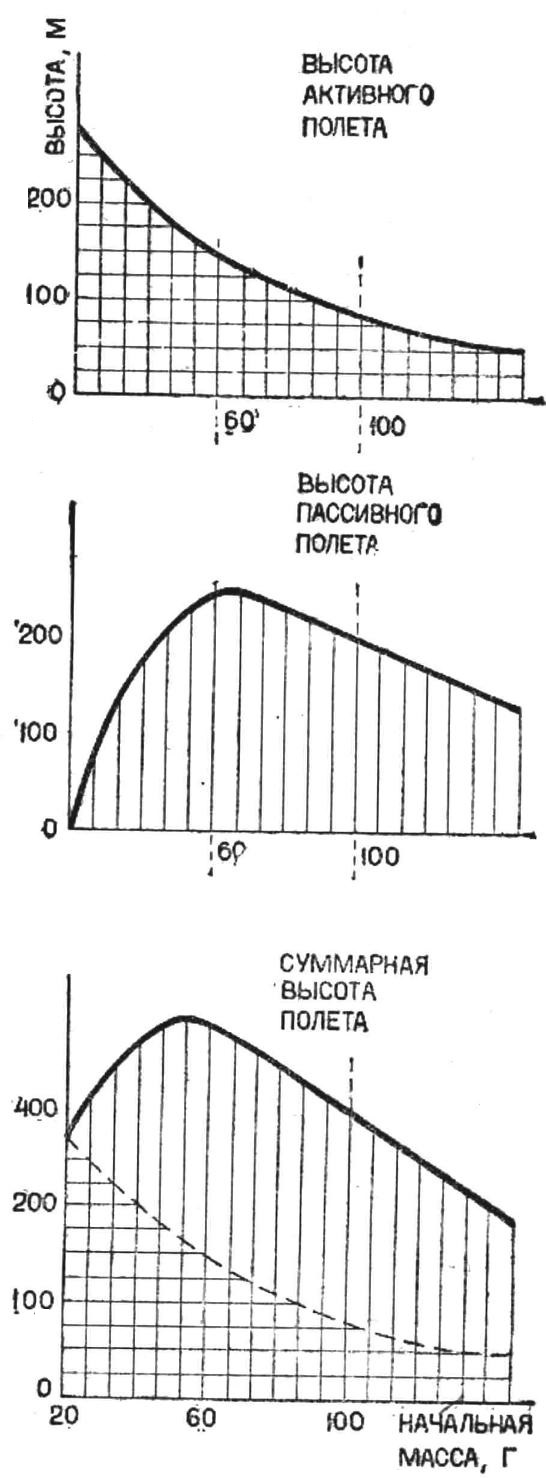
For illustration, we present the results of calculation of elevation models having different weights at the start (see Fig.). The trajectory is calculated by solving complicated differential equations on an electronic computer. For the calculation was taken one-stage model with a diameter of modelnogo section 22 mm and a drag coefficient of 0.75. The engine model has the full impulse of 10 N·s and creates a reactive force of 5 N for two seconds. The weight of fuel in the engine is 20 g. the Initial mass in the calculation was changed to compare the elevation models.
Graph A shows the height of active flight. With increasing initial mass of the rocket and a constant mass of fuel the ratio of the initial and final mass decreases. So, for the initial mass of 40 g is the ratio equal to 2, and 100 g -1,25. Accordingly, the height of the active rise in the first case is 200 m, while the second — 85 m, and the speed at the end of the active site — 160 km/h and 84 km/h.
Thus, the facilitation model leads to the increase in the height of active flight, and the greatest height will, if the whole rocket will consist of a single fuel, that is, to have mass at the start of 20 g. of Course, this option is unrealistic, but it is interesting as a limiting case of the lightest models. On schedule for a ultralight model, the active height of lift up to 245 m.
The limiting case of super-heavy model where a rocket will never be able to fly is a variant in which the final weight of the model will have more engine thrust. The estimated model, for example, do not fly during the initial weighing more than 500 g.
Referring now to the passive part of the trajectory (chart B]. How does the altitude of ballistic flight relief or weighting models? On this part of the mass of the rocket is constant and equal to the final (initial weight without fuel). You can use Newton’s second law, which States that the acceleration of a body is proportional to the force acting on it is proportional to the mass.
It is obvious that the rise of rockets on a passive site will be the higher, the smaller the acceleration it experiences under the action of forces of gravity and air resistance. Acceleration gravitational forces within the heights of the models can be considered constant. When the same resistance rocket with greater mass will experience a smaller acceleration and will rise to great heights.
So, the heavier the rocket at a constant rate at the end of the active site has a more extended section of passive recovery. But, unfortunately, we must note that with the weighting of the rocket the final speed EV active flight is reduced. Under the influence of these two factors, the height of the passive rise with increasing initial mass first increases and then decreases. For the estimated model, the height of passive recovery are greatest when starting weight equal to 65 g.
It is interesting to note that “ultralight” model does not have a passive station. Remember the mystery? “What can raise a baby, and athlete and across the Creek not being moved?” Answer: “A Feather”. Really, try to throw a feather: well she will not fly, however much it may throw. And for the model. If you make it too easy high, it will not rise, no matter what speed she nor reported at the end of the active site.
So, making it easier to model, we virtually deprive her of the possibility of passive flight, heavier — worsen the condition and result (final speed and altitude) active flight. Between these two extreme cases where something is the “Golden mean” model with the optimal initial weight. This mass can be defined for the analysis model according to the schedule, where the total height of the active and passive parts of the flight. She is 53 g, and the height of ascent is equal to 395 m. the lighter and heavier models have a lower height. The same height you can obtain and for light and heavy missiles. For example, a height of 345 m can be obtained for models with an initial mass of 30 g and 90 g.
So, the phenomenon of the “paradox light model” leads us to the conclusion that it is not always necessary to facilitate the model: weight of model in excess of the optimal values does not give a gain in height. The search for the optimal values of the starting mass of your model is one of the tasks of rakatomalala, the solution of which will allow him to achieve the best results in competitions.
V. KANAEV, engineer
Recommend to read
PUZZLE CRACKER
This lock is good for garage doors gate or even garage even from the inside, at least on the outside. It is durable, as massive, and has no arch, where the attacker can insert a...
RECUMBENT MADI
Invented and built unusual to our eyes the car of the students of the Moscow automobile and road Institute N. Belov, N. Dubinin, Yu Medovikov, A. Ortega-Gil and O. Khokhlova, under the...
